Помогнете на развитието на сайта, споделяйки статията с приятели!

За изчисляване на проблемите в електротехниката във физиката има редица правила, често използващи първия и втория закон на Кирххоф, както и закона на Ом. Германският учен Густав Кирххоф имаше постижения не само във физиката, но и в химията, теоретичната механика, термодинамиката. В електротехниката той използва модела, установен за електрическа верига, от две съотношения. Законите на Кирххоф (наричани още правила) описват разпределението на токовете в възлите и спада на напрежението върху елементите на схемата. По-нататък ще се опитаме да обясним на прост език как да приложим отношенията на Кирхоф за решаване на проблеми.

Първият закон на Кирххоф

Определението на първия закон е: " Алгебричната сума на токовете, преминаващи през възела, е нула." Може да се каже малко в различна форма: " Колко токове са изтичали в възела, същото количество е изтекло, което означава, че токът е постоянен . "

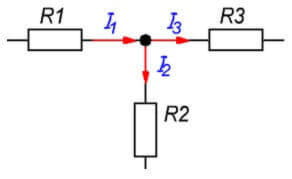
Верижният възел е точка на свързване на три или повече клона. Токовете в този случай се разпределят пропорционално на съпротивлението на всеки клон.

I 1 = I 2 + I 3

Тази форма на запис е валидна за DC вериги. Ако използвате първия закон на Kirchhoff за верига с променлив ток, тогава се използват моментни стойности на напрежения, обозначени с буквата İ и записани в сложна форма, като методът на изчисление остава същият:

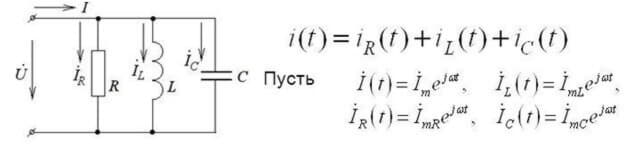
Сложната форма взема предвид както активните, така и реактивните компоненти.

Втори закон на Кирхоф

Ако първият описва разпределението на токовете в клоновете, то вторият закон на Кирххоф е: „ Сумата от паденията на напрежението във веригата е равна на сумата на всички ЕМП“. С прости думи, формулировката е: "ЕМП, приложена към секция на веригата, ще бъде разпределена по елементите на тази верига пропорционално на съпротивлението, т.е. според закона на Ом.

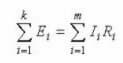
Докато за променлив ток звучи така: " Сумата от амплитудите на сложната едс е равна на сумата от сложните капки на напрежението на елементите . "

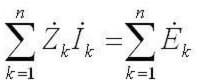
Z е импеданса или импеданса, той включва както резистивната част, така и реактивната част (индуктивност и капацитет), която зависи от честотата на променливия ток (има само активно съпротивление при постоянен ток). Следват формули за импеданс и индуктивност на кондензатора:

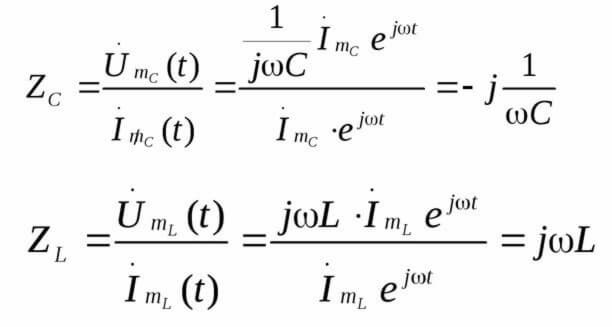
Ето снимка, илюстрираща горното:

След това:

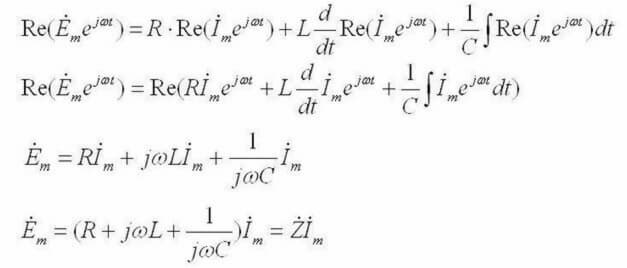
Методи за изчисляване на първия и втория закон на Kirchhoff

Да стигнем до практическото приложение на теоретичния материал. За да подредите правилно знаците в уравненията, трябва да изберете посоката на обхождане на контура. Вижте диаграмата:

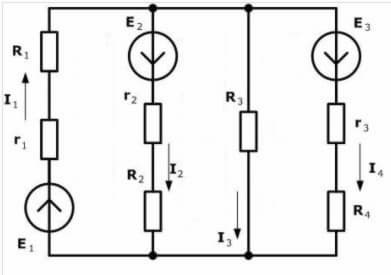
Предлагаме ви да изберете посока по часовниковата стрелка и да я посочите на фигурата:

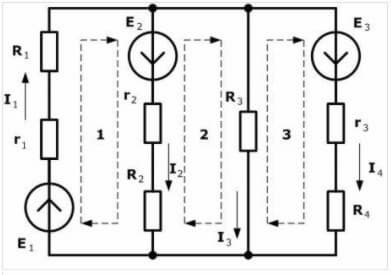
Линията на пунктирната линия показва как да следваме контура при изчертаване на уравнения.

Следващата стъпка е да се направят уравнения съгласно законите на Кирхоф. Първо използваме втория. Ние подреждаме знаците по следния начин: минус се поставя пред електромоторната сила, ако е насочен обратно на часовниковата стрелка (посоката, която избрахме в предходната стъпка), след което поставяме минус за едр по часовниковата стрелка. Ние правим за всеки контур, като вземаме под внимание знаците.

За първата, ние гледаме в посоката на ЕМП, тя съвпада с пунктираната линия, поставяме Е1 плюс Е2:

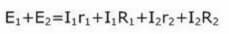
За второто:

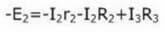
За третата:

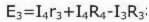
Знаците за IR (напрежение) зависят от посоката на контурните токове. Тук правилото на знаците е същото като в предишния случай.

IR се записва с положителен знак, ако токът тече в посоката на байпаса на веригата. И със знака "-", ако токът протича в посоката на байпаса на веригата.

Посоката на обходния байпас е конвенционална стойност. Тя е необходима само за поставянето на знаци в уравненията, тя е избрана произволно и не влияе на коректността на изчисленията. В някои случаи лошо избраната посока на ходене може да усложни изчислението, но това не е критично.

Помислете за друга верига:

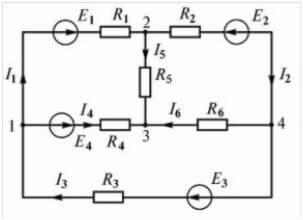
Тук има четири източника на ЕМП, но редът на изчисление е един и същ, първо избираме посоката за съставяне на уравненията.

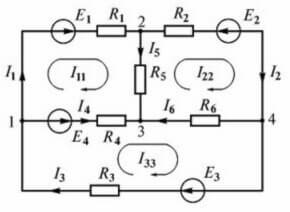
Сега трябва да направите уравнения според първия закон на Кирхоф. За първия възел (отляво на диаграмата е фигура 1):

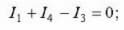
I 3 потоци в, и I 1, I 4 изтича, оттам и знаците. За второто:

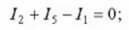
За третата:

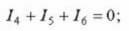
Въпрос: „Има четири възела и има само три уравнения, защо?”. Факт е, че броят на уравненията на първото правило на Кирхоф е равен на:

N уравнения = n възли -1

Т.е. има само 1 по-малко уравнение от възела, тъй като това е достатъчно, за да опише токовете във всички клонове, съветвам ви още веднъж да се издигнете до веригата и да проверите дали всички токове са написани в уравненията.

Сега ще се обърнем към конструирането на уравнения от второто правило. За първи контур:

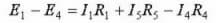
За втората верига:

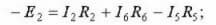
За третата верига:

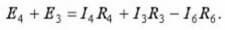
Ако заместим стойностите на реалните напрежения и съпротивления, тогава се оказва, че първият и вторият закон са валидни и изпълнени. Това са прости примери, на практика трябва да решите много по-обемни задачи.

Заключение. Основното в изчисленията, използвайки първия и втория закон на Кирхоф, е спазването на правилото за съставяне на уравнения, отчитат посоката на протичане на тока и трасето на веригата за правилното поставяне на знаците за всеки елемент от веригата.

Закони на Кирххоф за магнитна верига

Изчисленията на магнитните вериги са важни и в електротехниката, като и двата закона намират приложение и тук. Същността остава същата, но формата и величината се променят, да разгледаме този въпрос по-подробно. Първо трябва да разберете понятията.

Магнитомоторната сила (MDS) се определя от произведението на броя завъртания на намотката и тока през него:

F = w * I

Магнитното напрежение е произведението на силата на магнитното поле и тока в участъка, измерени в ампери:

U m = H * I

Или магнитен поток чрез магнитна съпротива:

U m = f * R m

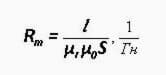
L е средната дължина на участъка, μ r и μ 0 са относителна и абсолютна магнитна проницаемост.

Създавайки аналогии, пишем първия закон на Кирххоф за магнитна верига:

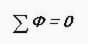
Това означава, че сумата от всички магнитни потоци през възела е нула. Забелязали ли сте, че звучи почти същото като за електрическа верига?

Тогава вторият закон на Кирхоф звучи като „Сумата на МДС в магнитна верига е равна на сумата от U M ­­ ­­ (магнитен стрес).

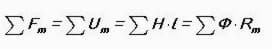
Магнитният поток е:

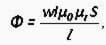
За променливо магнитно поле:

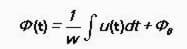
Тя зависи само от напрежението на намотката, но не и от параметрите на магнитната верига.

Като пример разгледайте следния контур:

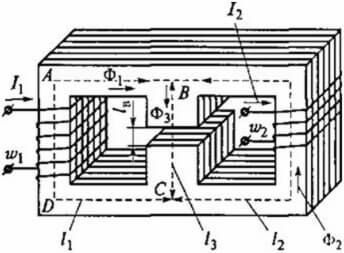
След това за ABCD получавате следната формула:

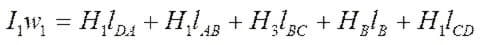
За контури с въздушна междина са изпълнени следните връзки:

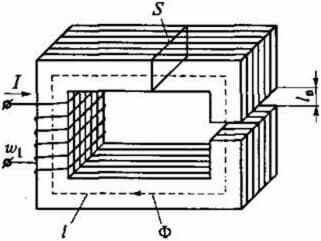
Магнитно съпротивление:

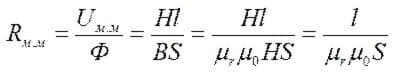
И съпротивлението на въздушната междина (отдясно на ядрото):

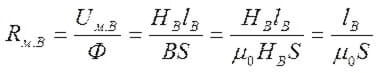
Където S е основната област.

За да разберете напълно материала и визуално да видите някои от нюансите на използването на правилата, препоръчваме ви да прочетете лекциите, предоставени на видеоклипа:

Откритията на Густав Кирххоф допринесоха значително за развитието на науката, особено на електротехниката. С тяхна помощ е много лесно да се изчисли електрическа или магнитна верига, токове в нея и напрежение. Надяваме се, че сега правилата на Kirchhoff за електрически и магнитни вериги са ви станали по-ясни.

Свързани материали:

  • Закон Joule-Lenz
  • Съпротивление на проводника спрямо температурата
  • Правилата на Gimlet с прости думи

Помогнете на развитието на сайта, споделяйки статията с приятели!

Категория:

Знание